CONSOMATONの話
こんにちは
TGA23のたもと申します。連日の投稿になりますが、今回はCONSOMATONというパズルゲームを紹介しようと思います。CONSOMATONは昨日の記事で紹介したMarkov Algorithm Onlineを二次元に拡張したようなゲームなのですが、難易度はむしろ下がっているので気軽にプレイできると思います。
遊び方
ゲーム画面を下に載せておきます。各ステージの目標は右上のCNSLと書かれた枠内(=とIで囲まれた部分)の文字列をある置換規則に従って置換していき、右下のGOALと書かれた枠内に一致させることです。左上のRULEと書かれた部分が置換規則であり、一度の置換では左側の3×3の文字列に一致する部分が右側の3×3に置き換わります。ただし、空白は空白文字として扱われるのではなく、任意の文字を表すワイルドカードとして解釈されます。たとえば、規則の左側が全て空白の場合は、任意の3×3の文字列に対して置換が実行されます(3×3が全て空白の部分のみが置換されるわけではない)。また、盤面は上下、左右ともに境界でループしています。
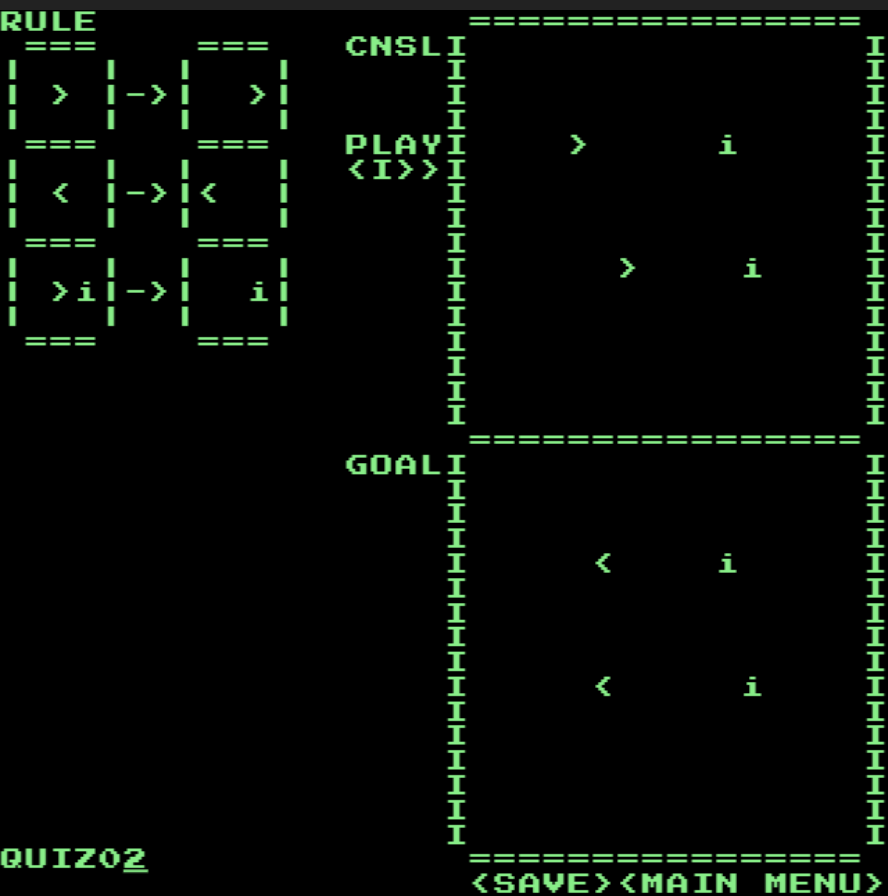
CONSOMATONには、通常のマルコフアルゴリズムとは異なり停止規則は存在しません。また、マルコフアルゴリズムでは置換規則や置換する文字列の位置に優先度が決まっており、各ステップでは最も優先度の高い置換が一度行われるのみでしたが、CONSOMATONでは各ステップにおいて、すべての規則が同時に作用し、かつ置換可能な対象をすべて置換します(競合する場合もありますが、上の規則から順に適用され、同じ規則による置換は左上からZ字を描くように行われるようです)。
具体例をもとに説明しましょう。初期状態でaを含まない盤面に対し下のような規則を実行した場合、最初のステップで左の盤面、次のステップで右の盤面、以降は1ステップごとに左右の盤面が切り替わります。

この場合どのように置換が行われるかというと、
1ステップ目
まず、一つ目の規則により盤面全体がaで埋まります。二つ目の規則は、初期状態にaが含まれないため置換が実行されません(規則が適用されるのは初期状態の盤面であり、一つ目の規則を適用した後の盤面ではないことに注意)。三つ目の規則も同様です。
2ステップ目
一つ目の規則により盤面全体がaで埋まります。次に、二つ目の規則により、すべてのaがbに置換され盤面全体がbに置き換わります。この結果は一つ目の規則による結果(盤面全体がaで埋まる)を上書きします。次に三つ目の規則ですが、ステップ開始時の盤面はすべてaで埋まっていたため、結局この規則は任意の3×3の部分に対して適用されることになります。置換を行う順番によって結果が変わりますが、左上からZ字を書くような順に処理が行われることから、結果として上図の右の盤面になります。この結果は、二つ目の規則による結果(盤面全体がbで埋まる)を上書きします。
3ステップ目
1ステップ目と同じ処理が行われます。以降同様に繰り返します。
以上がCONSOMATONのルールとなります。難しく思われるかもしれませんが、正解の規則の一部は初めから与えられているので、そこから推測すれば容易に解き進められると思います。
おすすめの問題
ここからは、個人的に面白かった問題をいくつか紹介します。
QUIZ07
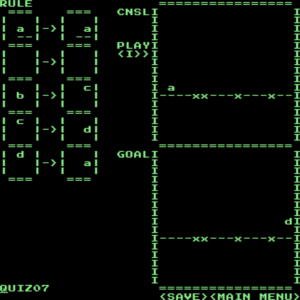
好き好んでこの記事を読むようなゲーム脳の皆様には説明するまでもないでしょう。マ〇オのごとく障害物を跳び越えろという問題です。CONSOMATONでは各問題の内容が事細かに説明されないので、こうして作者の意を酌む必要があるのが難しい点であり、最大の魅力でもあるのです。
解答(正攻法)
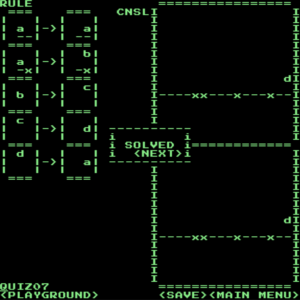
ちなみに、この問題は盤面が左右でループする仕様を悪用(?)し、以下のように1つの規則だけで解くこともできます。
解答(ズル)
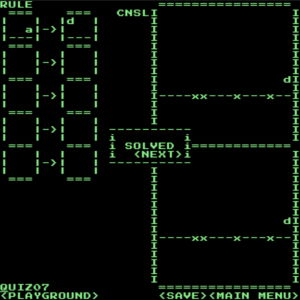
このように、製作者の意図を完全に無視した解き方を探すのもまた面白いです。
QUIZ10
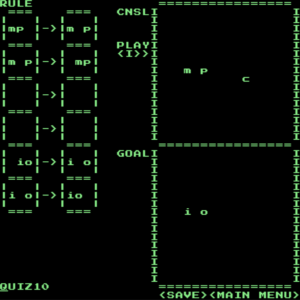
一見しただけでは分かりづらいですが、作者のブログによるとパ〇クマン的な動作を期待しているようです。つまり、初めはmから逃げていたpがcをとることによりその立場を逆転させ、逆向きに追いかける、というストーリーのようです。mがモンスター、pがパ〇クマン、cがパワーエサということですね。これを解答に落とし込むと下のようになります。
解答(正攻法)
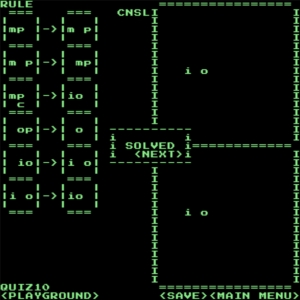
複数の規則が同時に適用されるという仕様上、上から3つ目の規則が適用されるタイミングでpが増えてしまうので、それを4つ目の規則で消す必要があるという、少しトリッキーな問題です。
作者がブログで嘆いていたように、下のようなズルい(?)解き方も存在します。問題の意図を理解できずに、こちらの解き方をした人も多いかもしれません。
解答(ズル?)
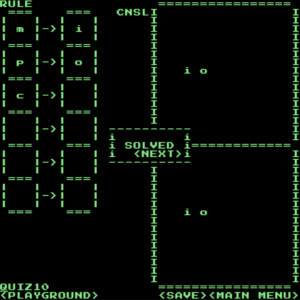
QUIZ17
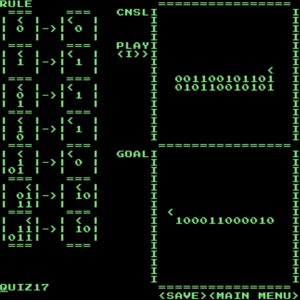
見ての通り、二進数の足し算をする問題です。解答は次の通りです。
解答(正攻法)
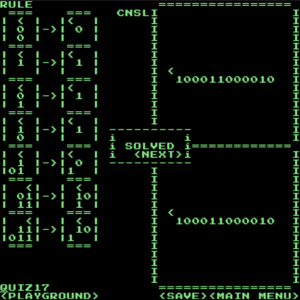
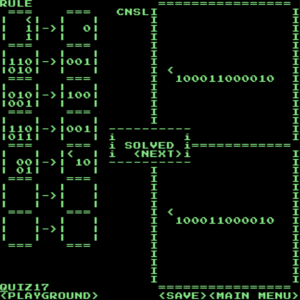
この解答は繰り上がりの処理に一般性がないですが、規則が8つあれば1桁同士の足し算の(繰り上がりを含めた)すべてのパターンに対応できるので、どれだけ桁数が増えても計算できるようになるはずです。なお、この問題でも下のようにズルできます。
解答(ズル)
おわりに
CONSOMATONはブラウザで気軽に遊べますし、問題もそこまで難しくないので頭の体操に最適です。ぜひプレイしてみてください。
