プログラムパズル_ハノイ 解説
この記事は、東京大学ゲーム研究会アドベントカレンダー2024、23日目の記事です。
はじめに
こんにちは。TGA23のたもです。本アドベントカレンダーに寄稿するのはこれで3回目になりますが、前の2本は軽めの記事だったので今回はガッツリ書きたいですね。
とか考えていたら公開日の前日になってしまいました。せっかくガッツリとネタを考えていたのに今から書いていたら間に合いません。僥倖、書くのは楽だけど読むのは大変な記事を書けば満足してもらえるのではないかと閃いたのでそうします。
というわけで、プログラムパズル_ハノイというちょっとしたパズルゲームの解説をします。
ゲーム紹介
名前の通り(擬似的な)プログラムを書いてハノイの塔を解くパズルです。穴埋め形式なのでプログラミングの知識はほぼ必要ないですが、穴埋めであるがゆえに作者の意図を汲み取る必要があり、下手に一からプログラムを書くより難しいです。
ところで、このゲームのサイト(よかひよかとき)には他にもパズルがたくさんあり、どれも頭を一捻り二捻りする必要があって面白いです。自分は、このサイトがフィルタリングに引っかからないのをいいことに中学時代に教室のパソコンで遊び倒していました。授業中に紙とペンで解いて友人と競い合っていたのが懐かしいです。
閑話休題。そもそもハノイの塔を知らない人もいるでしょう。ゲーム画面を拝借して説明します。

このパズルでは、3本の杭a, b, cと、互いにサイズが異なるn枚の円盤を使います。円盤の中央には穴が空いていて、杭に通せるようになっています。
はじめ、全ての円盤は杭aに上から小さい順に積み重なっています。プレイヤーは1手につき円盤を1枚ずつ他の杭に移すことができますが、自身よりサイズの小さい円盤の上に重ねることはできません。最終的に、すべての円盤を杭bに移すことができればクリアです。非常にシンプルですね。
ここから先、ネタバレ注意です。進む前にぜひ自力で解いてみてください。
Stage 1
最初のステージはハノイの塔の練習みたいなもので、どの円盤をどこに移すかを順に指定していくだけなのでプログラムもクソもありません。
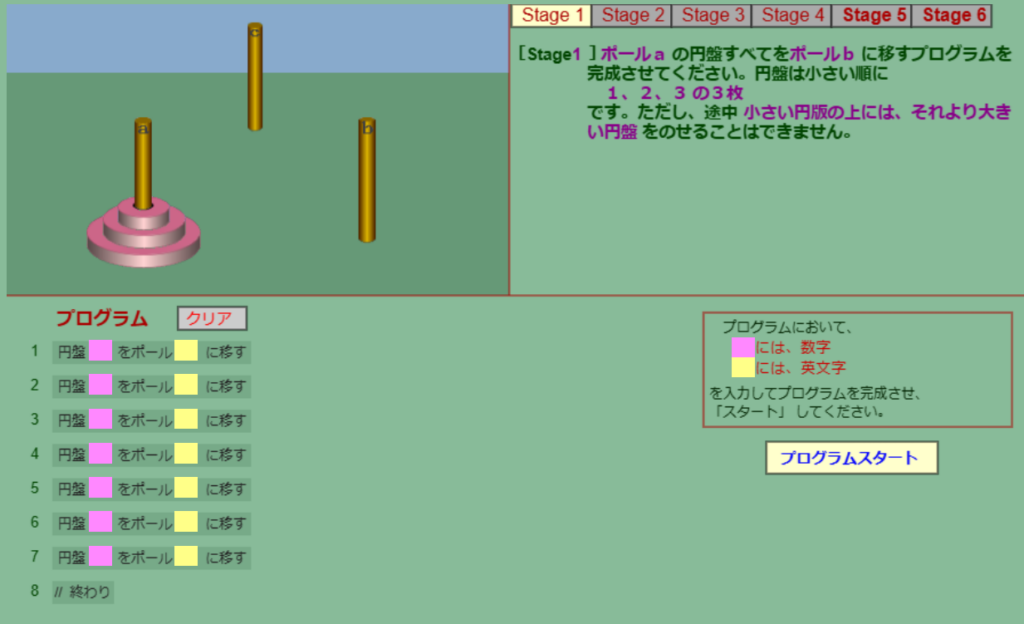
解答(クリックで展開)
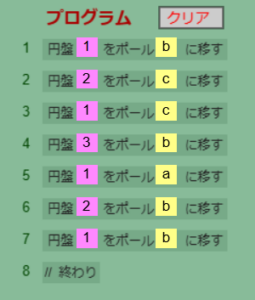
Stage 2
次のステージも内容はほぼ同じで、円盤が1枚増えただけです。

解答(クリックで展開)
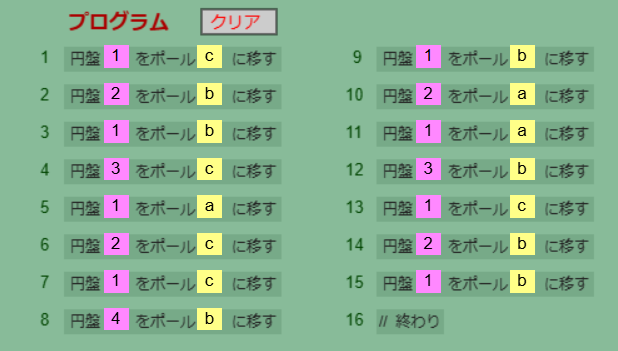
Stage 3
ここで一気に難易度が跳ね上がります。Stage 4、5はStage 3のマイナーチェンジで、Stage 6はガラリと傾向が変わりますがStage 3に比べると難易度は数段落ちます。つまり、Stage 3が実質的なラスボスです。とにかく問題を見てみましょう。
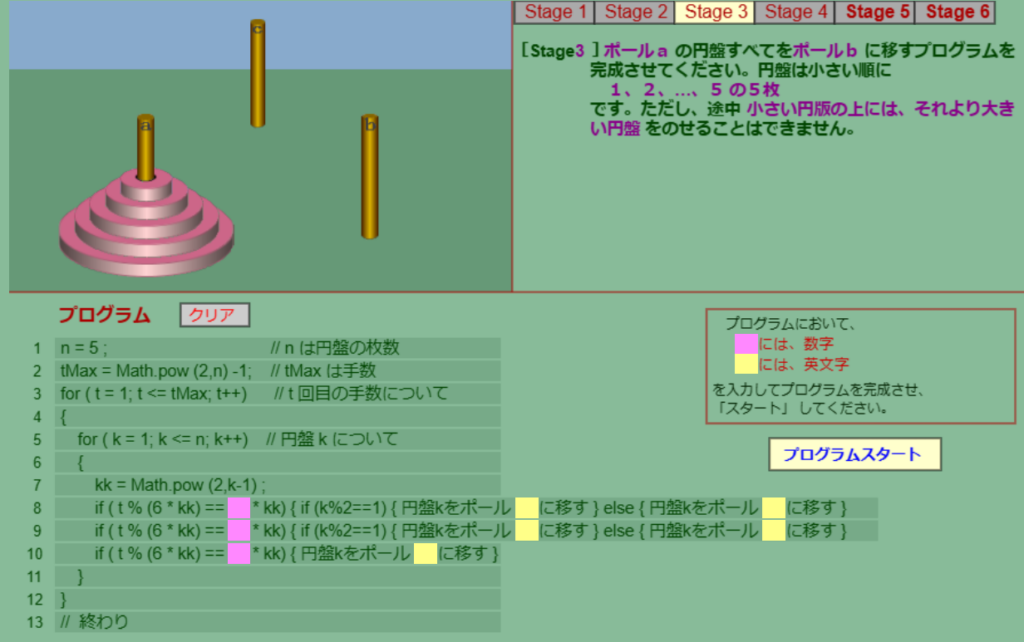
急に見た目がいかつくなりましたが、プログラム自体はさほど難しくないです。
この問題をいきなり解くのは難しいので、まずはハノイの塔自体の解き方を説明します。
ハノイの塔の解法
Stage1と2で勘の良い読者はお気づきになったかもしれませんが、円盤がn枚の時の最小手数は2n-1です。
略証:
n=1の時は明らか。
n=kのとき最小手数が2k-1であると仮定し、n=k+1について考える。円盤k+1を杭bに移すためには円盤1~kを全て杭cに移しておく必要があり、この操作に必要な最小手数は2k-1。その後円盤k+1を杭bに移すのに1手、円盤1~kを杭bに移すのに再度2k-1手かかるので、合計で2×(2k-1)+1=2k+1-1手で、これが最小。
あとは数学的帰納法を用いればよい。
さて、上の証明はハノイの塔の解き方を具体的に構成しているので、これをプログラムに落とし込めば良さそうです。
パズルの解法
まず、t手目にどの円盤を動かすかを考えましょう。
証明から分かる通りハノイの塔の解法は再帰的に構成できるので、円盤が1枚の場合から順に書き下していくと、円盤を動かす順序は
n=1 : 1
n=2 : 121
n=3 : 1213121
n=4 : 121312141213121
n=5 : 1213121412131215121312141213121
となります。これを見ると、円盤kを動かすのは
k=5 : 24手目
k=4 : 23手目、3×23手目
k=3 : 22手目、3×22手目、5×22手目、7×22手目
…
とわかります。一般化すると、円盤kを動かすのは t=2k-1×奇数 のとき、つまり t%2k=2k-1 のときです(%は剰余記号)。プログラムでは kk=2k-1と定義されているので、この条件は t%(2*kk) == kk と書けます。それっぽい形が出てきましたね。
さて、各tについてどの円盤を動かせばよいかは分かったので、あとはどの杭に動かせばよいかを考えればOKです。
まず、ハノイの塔を解く過程でそれぞれの円盤がどのように動くかを考えましょう。
k=n の場合、(a) → b のように動きます((a)はスタート地点)。
k=n-1の場合、円盤nをbに動かすために自身はcに逃げておく必要があるので、(a) → c → b のように動きます。
k=n-2 の場合も同様に考えると、 (a) → b → c → a → b のように動きます。
これを一般化すると、すべての円盤は
(a) → b → c → a → b → c → a … または (a) → c → b → a → c → b → a …
の動きをする(左右どちらのパターンかはkの偶奇で決まる)ことが分かります。
略証:
再帰性を考えると、円盤k+1のt回目の移動先と円盤kの2t回目の移動先は一致する。
よって、円盤k+1が (x) → y → z → x → …と動くとすると、
円盤kの動きは (x) → ○ → y → ○ → z → ○ → x → … となる。
○ には左右と異なる文字が入る(でなければ移動の意味がない)ので、結局
円盤kの動きは (x) → z → y → x → z → y → x → … となる。
あとはk=n-1を起点に帰納法を用いればよい。
円盤kを動かすのは t=2k-1×奇数 のときだったことを思い出すと、移動先は
t=2k-1×1, 2k-1×7, 2k-1×13, … のとき、杭b (杭c)
t=2k-1×3, 2k-1×9, 2k-1×15, … のとき、杭c (杭b)
t=2k-1×5, 2k-1×11, 2k-1×17, … のとき、杭a
となります。これも剰余とkkを用いて言い換えると、
t%(2k×3)=1×2k-1 ⇔ t%(kk*6)==1*kk のとき、杭b (杭c)
t%(2k×3)=3×2k-1 ⇔ t%(kk*6)==3*kk のとき、杭c (杭b)
t%(2k×3)=5×2k-1 ⇔ t%(kk*6)==5*kk のとき、杭a
となり、プログラムと同じ形が出てきました。完成したプログラムは次のとおりです。
解答(クリックで展開)

Stage 4
nが偶数になったバージョンです。

各円盤の最初の移動先(杭bか杭cか)が入れ替わるだけで、他は同じです。
解答(クリックで展開)

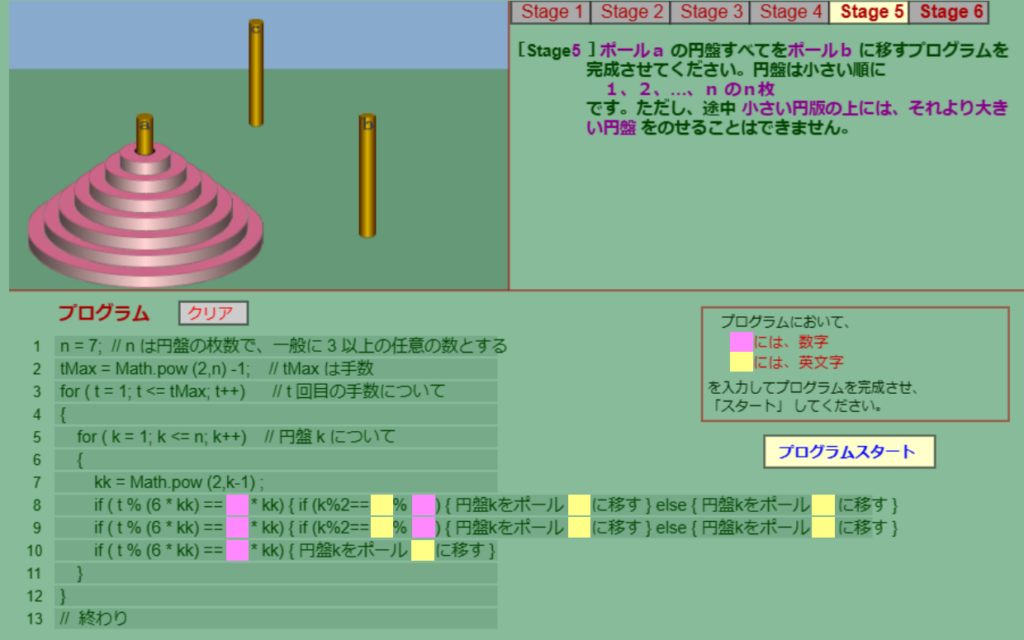
Stage 5
nが一般の正整数になったバージョンです。もう何をするかはお分かりでしょう。
Stage 5とStage 6に関しては正答者が名前を登録できるシステムがあるので、解答の掲載は控えておきます。
Stage 6
先に述べた通り、Stage 6はある意味独立した問題で、再帰関数を使います。
プログラムが急に簡潔になりましたが、そもそもハノイの塔が再帰的なものなので再帰関数と相性がいいわけです。こちらも解答は割愛しますが、ここまで読んでくださった方なら余裕でしょう。

終わりに
書くのが非常に大変でした。
